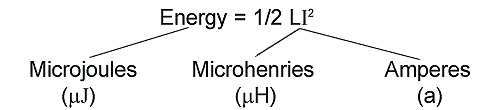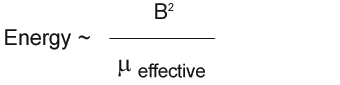Thermal aging is an irreversible increase in core loss as a result of prolonged exposure to elevated temperatures. The extent of these changes and realized effect on the wound core are a function of the following variables; time, ambient temperature and air flow, core volume and shape, operating frequency, peak ac flux density, material type and core manufacturer. Eddy current loss will be the dominant loss at higher frequencies while hysteresis loss will be the dominate loss at lower frequencies. The contribution of each form of loss to the total is also affected by the operating flux density. It is the eddy current portion of the core loss which is affected by high temperature thermal aging.

The first example will illustrate what happens in a design that is dominated by core loss and uses an undersized core. This design utilizes a core that can not safely dissipate the high level of core loss even with the benefit of forced air.

The first design example is for a buck inductor operating at 80 kHz. The parameters are as follows:

L = 11.5 μH
Idc = 18 A
E pk = 45 V
E dc = 12.3 V

The maximum ambient temperature is 60°C with forced air cooling supplied by a variable speed fan that provides less air flow at lower power levels.

The core selected is part number T106-52 wound with 14 turns of AWG-14 resulting in 1.72 W of copper loss. The peak AC flux density is 670 G at 80 kHz produces a core loss of 4.9 W. The combined loss is 6.62 W which calculates to a temperature rise of approximately 83C°in free standing air. Since the maximum ambient temperature specified for this part is 60°C the inductor can easily reach 140°C without the benefit of forced air. It should be noted that the core loss tolerances for CWS Bytemark cores are +/-15%. Under worst case core loss conditions, the 4.9 W nominal can be 5.64 W resulting in a total loss of 7.36 W for a temperature rise of 95C°in free standing air. These temperatures are much too hot for a core operating under these conditions where eddy current losses are a significant portion of the total loss. The T106 size core can safely dissipate a total of 2.59 W for a 40C°temperature rise.

Caution, a warning flag should go up on a design that is core loss dominated and depends on the use of air flow to reduce the temperature particularly if it uses a variable speed fan. While the copper loss will decrease at lower power levels, this is generally not the case with core loss. Variable speed fans should not be used with core loss dominated designs. It is much easier to remove heat from a copper loss dominated design than a core loss dominated design. The copper winding radiates the heat while the core material has a thermal impedance barrier that must first be overcome. Additionally, the inductor can be several degrees hotter on the inside of the core and in the "shadow of the air flow".

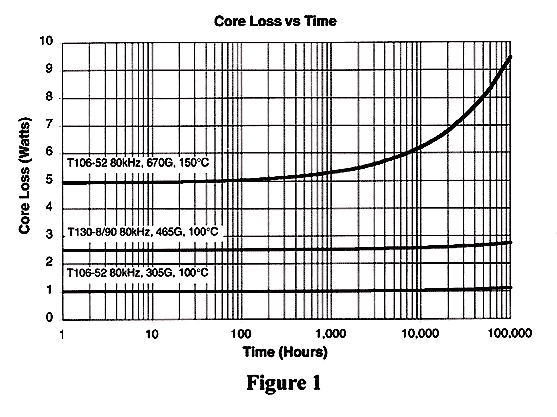
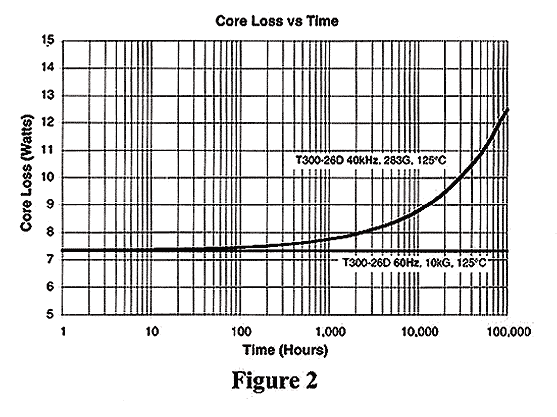
The upper curve in Figure 1 illustrates how quickly the projected core loss increases due to the excessive operating temperature. It should be obvious the surface area of this design is much too small to safely dissipate the excessive core loss in spite air flow. The Single Layer Winding Table and "Full Winding" Table show the "Total Power Dissipation (W) Vs Temperature Rise" for various sized Micrometals cores. These tables are useful to quickly determine if the design is capable of meeting a 40C°or less temperature rise.

The middle curve in Figure 1 illustrates the smallest physical core size that meets the design requirements and has a temperature rise of less than 40C°. This core is part number T130-8/90 wound with 19 turns of AWG-10 for a copper loss of about 1.0 W. The peak AC flux density has been reduced to 465 G at 80 kHz decreasing the core loss to 2.5 W. The graph predicts this design will safely operate at 100°C total temperature well past 100,000 hours.

The lower curve of Figure 1 shows part number T106-52 used under similar conditions to the first design except now the dc output voltage is 5 V instead of 12.3 V. With 14 turns of AWG-12 wire, the peak AC flux density has decreased to 305 G and core loss to 1.0 W. The combined core and copper losses are 2.04 W for a temperature rise of 33C°. This design will safely operate at 100°C total temperature for more than 100,000 hours.

The next design examples will illustrate differences using a much larger core size, operating at two differing frequencies and peak AC flux densities. The first design is operating at 60Hz, 10 kG on Micrometals part number T300-26D. The calculated core loss is about 7.35 W and assuming a copper loss of 7.35 W, the combined loss of 14.7 W results in a 33C° temperature rise. The lower curve in Figure 2 predicts that the core loss does not change even after 100,000 hours at 125°C. Almost all of the core loss at this frequency is hysteresis loss and is unaffected at this temperature.

The upper curve in Figure 2 shows how quickly the core loss increases in a design operating at 40 kHz with a peak AC flux density of 283 G. While the total core loss of 7.35 W is the same as the 60 Hz example, the eddy current losses are now dominant and increase with constant exposure to 125°C.

Assuming the copper loss is 7.35 W, the total loss of this design is 14.7 W resulting in a temperature rise of 33C°at time zero. After 20,000 hours the core loss has increased to 9.5 W and the temperature rise now reaches 37C°. After 100,000 hours at 125°C, the core loss has increased to 12.5 W, pushing the temperature rise to 42C°. This design example is not an extreme case but illustrates how the temperature rise of the inductor continues to increase as a function of time and temperature.

Another popular application for iron powder cores is power factor correction boost chokes. This can be a very demanding application where core loss calculation is more complex and often misunderstood. This can lead to poor designs that will have reliability problems. For a detailed discussion of proper core loss analysis for PFC boost chokes refer to Power Factor Boost Preregulator Core Loss Calculations. Also, the latest version of CWS Bytemark design software includes a PFC core loss application.

TABLE 1
	Solution #1	Solution #2	Solution #3
Part Number	E168-52	E168-52	E168-2
AL (nH/N2)	179	179	44
Turns	45	90	76
AWG#	14	17	16
Bpk @ 100 kHz (G)	389	195	230
Core Loss (mW/cm3)	489.0	120.0	61.5
Core Volume (cm3)	18.5	18.5	18.5
Core Loss (mW)	9,063	2,220	1,137
Copper Loss (mW)	866	3,480	2,324
Total Loss (mW)	9,929	5,700	3,461
Wound Surface Area (cm2)	66.7	66.7	66.7
Maximum Size (in)	1.7 x 1.7	1.7 x 1.7	1.7 x 1.7
T (C°)	65	41	27
Approx. Core Cost (per piece)	$0.23	$0.23	$0.55
Thermal Life (Hours)	<12,000	~1,000,000	>10,000,000

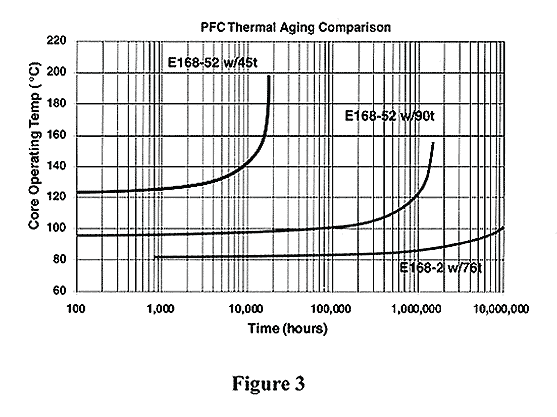
The third design example is a PFC boost choke operating at 100 kHz with the following requirements: Lmin = 250 μH
Idc = 7 A
Epk In = 120V
Edc Out = 400V

Referring to Table 1, you can see that design Solution #1 is a design that is dominated by 9.06 watts of core loss with only 0.87 watts of copper loss. This results in a temperature rise of 65C°. Figure 3 indicates that with an ambient of 55°C, this part will have thermal runaway in less than 2 years.

Solution #2 demonstrates that with the same core, by simply increasing the number of turns with the required smaller wire size, the core and copper losses will become more balanced. This results in improved efficiency (saving 4.3 watts), a lower operating temperature (DT=41C°), and a dramatic improvement in thermal life (almost 2 orders of magnitude). While it may seem obvious that solution #1 is a poor design, this is a fairly common mistake.

If the higher inductance produced by adding turns in solution #2 is unacceptable in the circuit, the core and copper losses can also be better balance by selecting a lower permeability material. Solution #3 illustrates how the Micrometals 10μo (-2 Material) performs. This choke will be the most efficient and reliable, but this material type is more expensive than the –52 Material option.

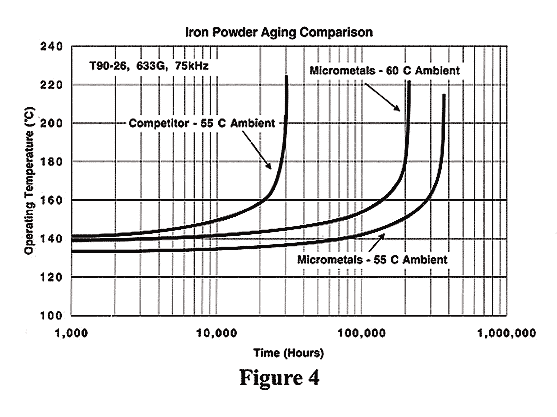
Another important thermal aging consideration is the source of the iron powder cores, in other words, beware of "equivalent" iron powder cores. As demonstrated above, different materials will thermally age at different rates. This is also true with different manufacturers of core materials. In many cases, the term "equivalent core" is solely based on dimensional and permeability characteristics.

Figure 4 illustrates the thermal aging characteristic of CWS Bytemark T90-26 at 75kHz with 633G as well as the same winding on an "equivalent" competitor. The CWS Bytemark core will safely operate for 300,000 hours whereas the competitor will runaway in less than 30,000 hours. Clearly, both cores are thermally aging at different rates. temperature rise of 65C°.

Less obvious is the variation of initial core operating temperatures between the CWS Bytemark and competitor cores. The competitors increased initial core temperature is a result of higher core losses. In another example, the ambient temperature for the CWS Bytemark winding was increased to 60°C to match the initial core operating temperature of the competitor. Again, the predicted difference in thermal life is dramatic.

As the example above demonstrate, evaluating one manufacturers core and substituting another at a later time can be a critical error. It is also very important to regulate the supply chain and monitor that sub-suppliers are not making any unknown core substitutions.

DC energy storage inductors are an ideal application for CWS Bytemark iron powder cores. In this application the core must support a significant DC current while maintaining an inductance adequate to filter high frequency signals. The amount of energy stored is a function of inductance and current. Specifically, energy storage for an inductor is described:

Energy storage is proportional to the flux density squared divided by the effective premeability of the structure.

The introduction of a discreet air gap significantly lowers the effective permeability of core structures made from ferrites and iron alloys. This increases the energy storage capabilities of the core by allowing additional energy to be stored in the gap.

1. Those specifically designed to maintain a relatively constant inductance from zero to full-rated load.
2. Those specifically designed to have greater inductance, under minimum load conditions (swing).
3. Those simply requiring a minimum inductance.

Micrometals Energy Storage Curves are presented for a number of core sizes in each material (except -2 Material due to its low permeability) to assist in the design of such inductors. These curves are shown a both in terms of ampere-turns (NI) on each materials page, and percent saturation (100% -% initial permeability) on each materials page.

The curves shown for each material are based on a peak AC flux density of 10 gauss (1 mT). This will typically represent a ripple current of less than 1%. Under this condition, the only heat generated results from the resistive winding (copper) losses. The energy storage limits for 10 C°, 25 C°, and 40 C° temperature rise (in free-standing air) resulting from winding losses are shown on each graph. When significantly greater AC or ripple flux density is present, the cores will produce higher inductance due to the AC magnetization characteristics shown Peak AC Flux Density on percent initial permeability. Under this condition, the high frequency core losses must also be taken into account as described Core Loss. Refer to Power Factor Boost Preregulator Core Loss Calculations for additional information.

The -8 , -18 and -52 Materials should be considered for DC chokes operating above 100kHz due to their lower core loss characteristics at high frequency.

The importance of the swing of the inductor must be determined before the appropriate core material can be selected.

1. The -8, -18, -30, -34 and -35 Materials ( or a gapped E Core, see Gapping Iron Powder E Cores) should be considered if the inductor must maintain a relatively constant inductance from minimum to full-rated current. These materials are able to store high energy with a minimum of staturation.
2. The -26, -40, -45 and -52 materials should be considered if the inductor should "swing" (increase in inductance as current decreases) a moderate amount. These materials have higher permeability and can produce a 2:1 swing (50% saturation point).
3. The -26, -40 and -52 Materials are generally recommended for designs concerned with minimum inductance because they are the most cost effective.

The temperature rise of the wound unit, aside from saturation, is the primary limiting factor in inductor design. In the case of DC inductors with very low level AC ripple, this temperature rise is a result of copper loss in the winding. (DC flux does not have a noticeable effect on core loss.)

For single-layer windings on toroidal cores, the current handling capability of a wire size as a function of temperature rise is relatively independent of core size. Making use of this, a single-layer winding table has been developed giving current ratings for temperature rises of 0C°, 25C°, and 40C° temperature rise in free-standing air. The Single Layer Winding Table

For full windings (45% toroid inside diameter remaining) a similar table has been developed, "Full Winding" Table.In the case of full windings, the current handling capability of a given wire size is no longer independent of core size. However, for any particular core size, an ampere-turn rating for a given temperature rise does become a constant. These ampere-turn constants are included in the "Full Winding" Table.

Refer to-26 Material for design examples using the Energy Storage Curves.